III. Thuật toán AES - thực hiện

Trong phần này chúng ta sẽ tìm hiểu kỹ hơn về từng công việc được thực hiện trong quá trình mã hóa, giải mã của thuật toán AES. Bao gồm cách xử lý, thao tác với khối dữ liệu, secret key, từng bước thực hiện trong mỗi round mã hóa. Loại thuật toán AES xét đến là AES-128.

1. Thao tác với khối dữ liệu

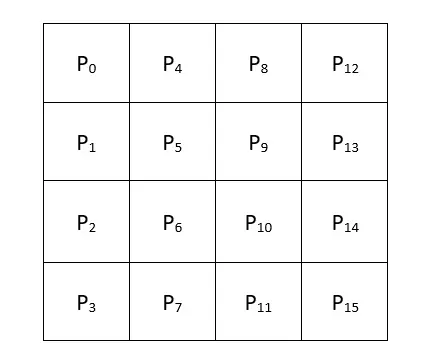
AES-128 chia văn bản cần mã hóa thành các nhóm dữ liệu, mỗi nhóm dữ liệu có độ lớn $128$ bit hay $16$ byte. Mỗi nhóm này được chuyển thể thành một ma trận $4\times4$, thể hiện dưới dạng một khối (block). Trong đó mỗi $P_i$ $(i = \overline{0,15})$ có độ lớn $1$ byte, được sắp xếp theo thứ tự từ trên xuống dưới, từ trái qua phải.

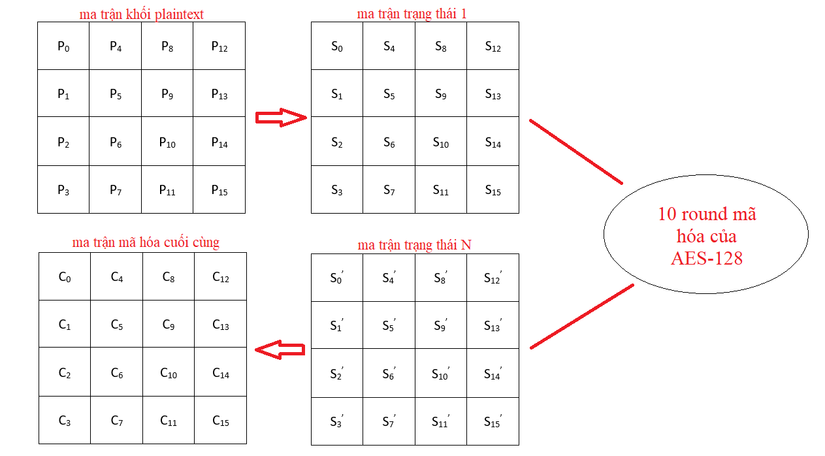
Trong mỗi round mã hóa, các khối này được thể hiện dưới dạng ma trận trạng thái (state matrix). Ma trận trạng thái thay đổi giá trị sau mỗi round mã hóa. Kết quả cuối cùng của ma trận này cũng chính là ma trận của văn bản mã hóa. Quan sát kỹ hơn qua sơ đồ dưới đây:

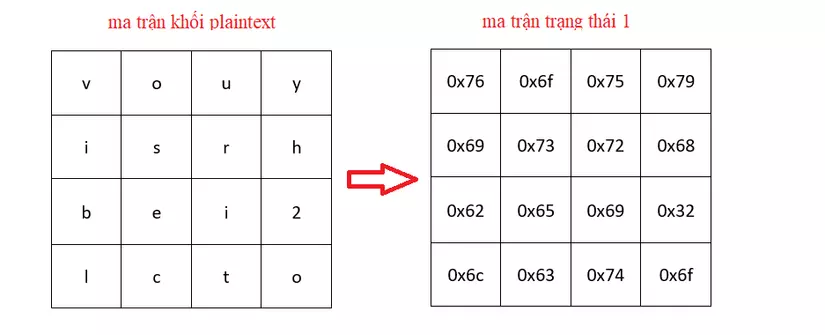
Ví dụ, với block viblosecurityh2o, khi biểu diễn lần đầu với ma trận trạng thái, chúng ta có state table $1$ (biểu diễn ở dạng hex):

Khi thực hiện trong chương trình, chúng ta thường sử dụng một list với $4$ phần tử list (mỗi phần tử list này chứa $4$ phần tử) biểu thị cho $16$ byte.

matrix = [[], [], [], []]

Để thuận tiện cho các bước tính toán ở các bước sau, chương trình thường quy ước phần tử thứ i của list matrix tương ứng với các phần tử cột i của block. Ví dụ với block trên chúng ta có biến matrix mang giá trị:

matrix = [['v', 'i', 'b', 'l'],
          ['o', 's', 'e', 'c'],
          ['u', 'r', 'i', 't'],
          ['y', 'h', '2', 'o']]

Với quy ước như trên, hàm chuyển đổi từ bytes sang block có thể dễ dàng thực hiện như sau:

def bytes2matrix1(text):
    """ Converts a 16-byte array into a 4x4 matrix.  """
    return [list(text[i:i+4]) for i in range(0, len(text), 4)]

Đối với quá trình giải mã ngược lại, các bạn cần đưa các phần tử từ block trở về chuỗi byte. Có thể luyện tập với challenge Structure of AES. Mục đích là hoàn thiện hàm matrix2bytes() chuyển thể ngược lại từ ma trận trở về chuỗi byte dựa vào hàm bytes2matrix() được đề bài đưa ra:

def bytes2matrix(text):
    """ Converts a 16-byte array into a 4x4 matrix.  """
    return [list(text[i:i+4]) for i in range(0, len(text), 4)]

def matrix2bytes(matrix):
    """ Converts a 4x4 matrix into a 16-byte array.  """
    ????

matrix = [
    [99, 114, 121, 112],
    [116, 111, 123, 105],
    [110, 109, 97, 116],
    [114, 105, 120, 125],
]

print(matrix2bytes(matrix))

2. Thao tác với khóa - AES key schedule

Như chúng ta đã biết, trong mã hóa AES dữ liệu được đưa vào các vòng (round) mã hóa liên tục, số round mã hóa phụ thuộc vào loại mật mã AES sử dụng. Secret key $128$ bit sẽ được sử dụng trong mỗi vòng mã hóa. Mỗi round cần một khóa có độ dài $128$ bit. Tuy nhiên, không phải tất cả các round đều sử dụng cùng một secret key. Vậy thì, chỉ với một secret key có độ dài $128$ bit, làm sao để có thể sử dụng cho các round mã hóa (mỗi round cũng cần một key dài $128$ bit) mà không bị trùng lặp? Lúc này chúng ta cần thực hiện một thao tác có tên gọi: Expand key - mở rộng khóa.

2.1. Round constants

Round constants định nghĩa các mảng $rcon_i$ $(i = \overline{1,10})$. Trong đó mỗi mảng $rcon_i$ bao gồm $4$ phần tử, mỗi phần tử có độ lớn $8$ bit.

$$rcon_i = [rc_i\ \ 00_{16}\ \ 00_{16}\ \ 00_{16}]$$

Giá trị $rc_i$ $(i = \overline{1,10})$ được tính toán như sau:

$$rc_i= \begin{cases} 1&\text{nếu }\ i = 1\\ 2\cdot rc_{i-1}&\text{nếu }i > 1 \text{ và } rc_{i-1} < 80_{16}\\ (2\cdot rc_{i-1})\ \oplus\ 11B_{16}& \text{nếu } i > 1 \text{ và } rc_{i-1} \ge 80_{16} \end{cases}$$

Như vậy, chúng ta có $10$ giá trị của $rc_i$ được liệt kê trong bảng sau:

2.2. The key schedule

Tương tự như trên, secret key được chuyển thể thành một ma trận $4\times 4$ sắp xếp từng byte theo thứ tự từ trên xuống dưới, từ trái sang phải. Ví dụ với khóa $K_0K_1K_2...K_{15}$ chúng ta có block:

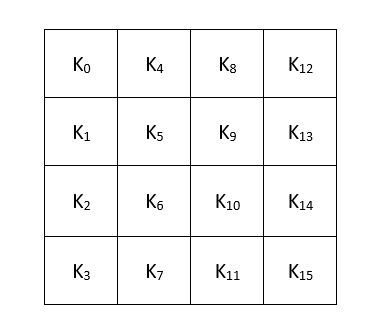
Trước khi đến với kỹ thuật expand key, chúng ta cần tìm hiểu một số định nghĩa.

Trong ma trận $4\times 4$ trên, định nghĩa mỗi cột là một "từ" có độ dài $32$ bit ($32$-bit word).

Hàm $RotWord()$ thực hiện "dịch byte" của mảng $32$ bit sang bên trái một vị trí. Cụ thể:

$$RotWord([b_0\ b_1\ b_2\ b_3]) = [b_1\ b_2\ b_3\ b_0]$$

Hàm $SubWord()$ thực hiện thay thế các byte trong mảng $32$ bit thành các giá trị tương ứng định quy định trong bảng S-box (Khái niệm sẽ tìm hiểu kỹ hơn trong phần sau). Cụ thể:

$$SubWord([b_0\ b_1\ b_2\ b_3]) = [S(b_0)\ S(b_1)\ S(b_2)\ S(b_3)]$$

Secret key sẽ được mở rộng thành một chuỗi tạo bởi $44$ word, ký hiệu là $W[0], W[1], W[2], ..., W[43]$. Với $W[0], W[1], W[2], W[3]$ lần lượt tạo bởi bốn cột của secret key gốc. Các word từ $W[4]$ đến $W[43]$ được tính toán dựa vào các hàm định nghĩa trên. Tổng quát, chúng ta có quy tắc tính toán các word trong expand key:

$$W_i = \begin{cases} K_i & \text{if } i < N \\ W_{i-N} \oplus \operatorname{SubWord}(\operatorname{RotWord}(W_{i-1})) \oplus rcon_{i/N} & \text {nếu } i \ge N \text{ và } i \equiv 0 \pmod{N} \\ W_{i-N} \oplus \operatorname{SubWord}(W_{i-1}) & \text{nếu } i \ge N \text{, } N > 6 \text{, và } i \equiv 4 \pmod{N} \\ W_{i-N} \oplus W_{i-1} & \text{Các trường hợp còn lại} \\ \end{cases}$$

Như vậy, đối với loại mật mã AES-128, với secret key có độ dài $128$ ban đầu sẽ được mở rộng thành $11$ nhóm key mới, mỗi nhóm chứa $4$ word (tổng $44$ word như đã nêu trên). Từng nhóm key này sẽ được sử dụng trong mỗi round trong cả quá trình mã hóa và giải mã AES.

Về cách thực hiện tổng quát expand key với loại mật mã AES bất kỳ, bạn đọc có thể tham khảo thêm tại https://en.wikipedia.org/wiki/AES_key_schedule.

3. Tổng quan các round mã hóa và giải mã trong AES-128

Đối với AES-128, quá trình mã hóa thực hiện tổng $10$ vòng (rounds). Có $4$ loại công việc được thực hiện và tạo thành các round này là: AddRoundKey, SubBytes, ShiftRows, MixColumns. Về cụ thể các công việc thực hiện trong mỗi loại sẽ được giới thiệu kỹ hơn trong phần sau. Tổng quan quá trình mã hóa có thể quan sát qua sơ đồ sau:

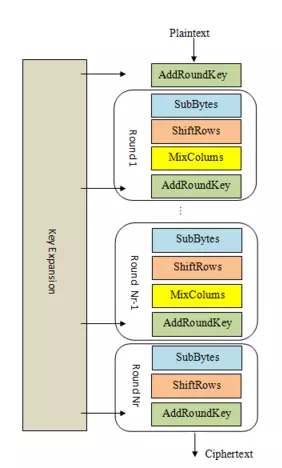(Sơ đồ tổng quát với mật mã AES, trong trường hợp này Nr = 10)

Trước khi đi vào round đầu tiên, thuật toán thực AddRoundKey đối với block, sau đó từ round $1$ tới round $9$ thực hiện nhóm công việc lần lượt theo thứ tự: SubBytes, ShiftRows, MixColumns, AddRoundKey. Riêng round cuối cùng chỉ thực hiện $3$ công việc SubBytes, ShiftRows, AddRoundKey.

Các nhóm secret key sau khi mở rộng sẽ được sử dụng trong duy nhất loại công việc AddRoundKey. Như các bạn thấy, có $11$ lần AddRoundKey, cũng là lý do vì sao khóa được mở rộng thành $11$ nhóm.

Quá trình giải mã thực hiện ngược lại lần lượt các công việc trong mã hóa, với quy ước các round gồm nhóm công việc thay đổi một chút:

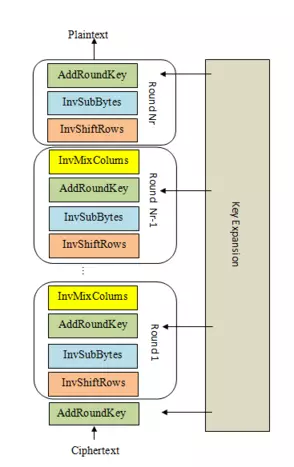
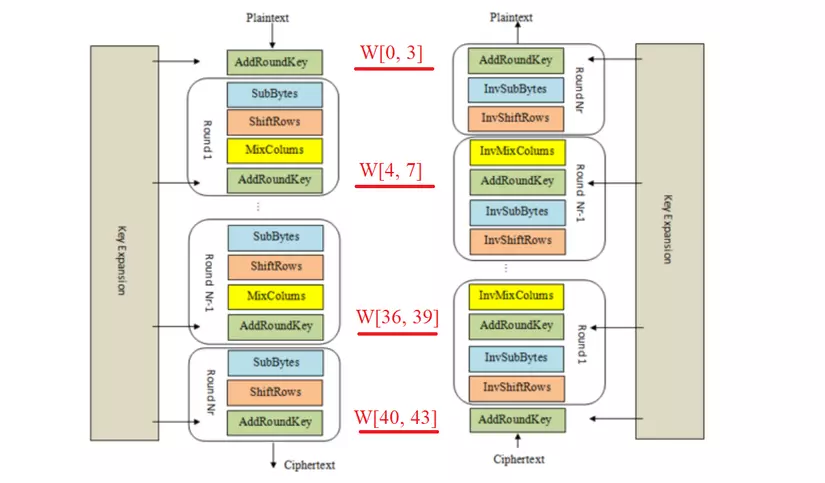
Bạn đọc có thể quan sát sơ đồ tổng quát sau cho thấy các nhóm word trong expand key được sử dụng tương ứng trong quá trình mã hóa và giải mã:

Tài liệu tham khảo

• https://en.wikipedia.org/wiki/Advanced_Encryption_Standard
• https://www.geeksforgeeks.org/advanced-encryption-standard-aes/
• https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.197.pdf
• https://en.wikipedia.org/wiki/AES_key_schedule