Mật mã RSA - phần 5
V. Thuật toán Pollard (tiếp)
2. Tấn công phân tích nhân tử theo thuật toán Pollard Rho (Pollard )
2.1. Thuật toán Pollard
Xét số là tích của hai số nguyên tố lớn và . Tương tự với ý tưởng của thuật toán Pollard's , để tìm được một ước nguyên tố của , chúng ta sẽ tìm kiếm hai số nguyên dương và không vượt quá và thỏa mãn:
Vì khi đó , mà nên . Từ đó:
Hay chắc chắn là một ước (khác ) của . Bài toán trở về tìm một ước nguyên tố của . Độ khó của bài toán mới này có tăng lên không, sẽ phụ thuộc vào cách chúng ta chọn được cặp số ra sao (vì bài toán tìm ước chúng lớn nhất có thể giải quyết dễ dàng bằng thuật toán Euclid).
Một ý tưởng đơn giản có thể thực hiện để giải quyết vấn đề này như sau: chọn ra tập chứa các số nguyên không vượt quá . Chúng ta quan tâm tới việc tìm ra hai phần tử sao cho , hay . Xét ánh xạ , với xác suất tồn tại hai phần tử có cùng ánh xạ đích từ trở lên, theo nghịch lý ngày sinh nhật thì chúng ta chỉ cần chọn ra tập có số phần tử . Tuy nhiên, để tìm được sự "trùng ánh xạ" này trong tập , số lần tính toán ước chung lớn nhất cần thực hiện là:
Lúc này, cách thực hiện của thuật toán Pollard giúp chúng ta giảm đi số lần tính toán GCD. Thay vì sinh ngẫu nhiên một tập , thuật toán sẽ chọn các phần tử theo quy tắc. Xét là một đa thức hệ số nguyên, đầu tiên, chọn là một số nguyên nhỏ hơn , lần lượt xác định:
Cuối cùng thu được tập . Cụ thể vì sao cách chọn này có thể giảm số lần tính GCD như đã nêu, cùng theo dõi các tính chất sau.
Giả sử có (mục tiêu chúng ta hướng tới), do là đa thức hệ số nguyên nên cũng sẽ có .
Do và là một ước của nên:
Tương tự có nên suy ra
Tổng quát: Nếu có thì có: (tính chất *)
Từ đây có thể thấy, khi liên tục tính từ (lưu ý theo định nghĩa phía trên chúng ta đang tính theo module ), và nhìn theo một dãy số mới qua module , dần dần chúng ta sẽ đi vào một vòng lặp tuần hoàn:
Để hình dung dễ hơn về vòng lặp này, xét ví dụ: , , chọn . Tính được số hạng đầu của tập là:
# f(x) = x*x + 1
def f(i, n):
if i == 1:
return 1
return (f(i - 1, n) * f(i - 1, n) + 1) % n
Viết lại dãy này thành một dãy mới theo module có hình dạng như sau:
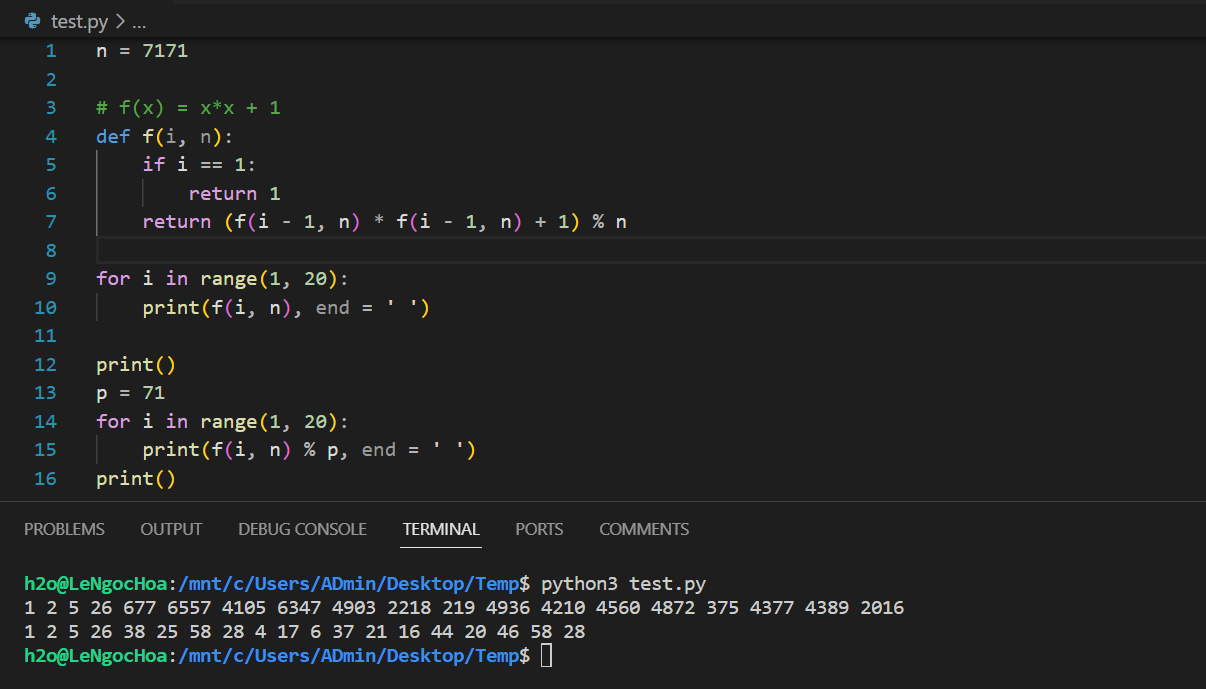
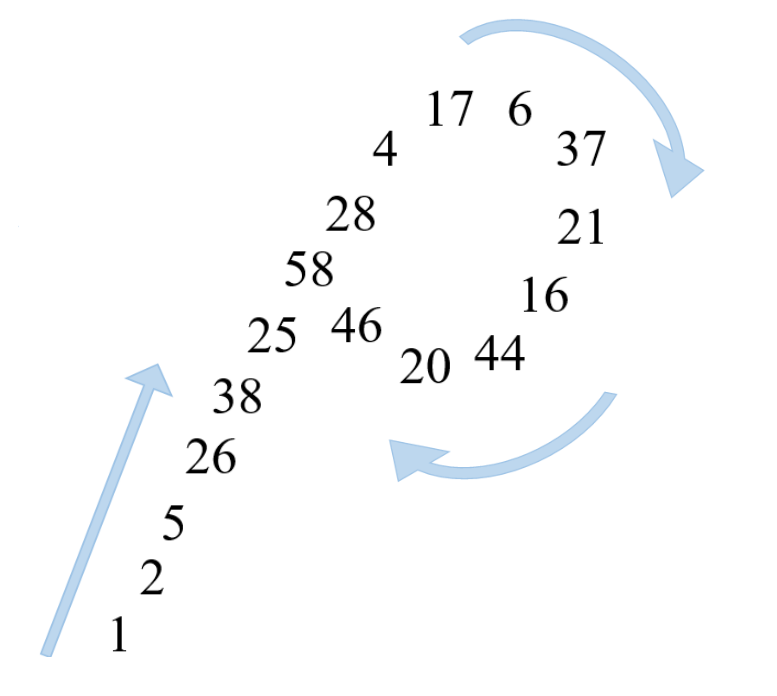
Do hình dạng lặp lại tương tự ký tự nên Pollard đã đặt tên là thuật toán Pollard . Từ hình trên có thể thấy . Túc là bằng việc tính toán liên tục có thể thu được là một ước nguyên tố của .
Lúc này, chú ý rằng thời gian và tài nguyên sử dụng cho việc tìm ra số nguyên tố dựa vào số lần tính toán với cặp số chọn từ trong tập . Như vậy chiến thuật thực hiện tính toán là rất quan trọng!
Chẳng hạn, mỗi khi tập có thêm một thành viên mới thì chúng ta sẽ cần tính lần GCD tương ứng với cặp . Để gặp được cặp là kết quả mong đợi, chúng ta cần thực hiện lần tính toán.
Tuy nhiên, nếu tục tính thêm phần tử mới cho , do đi vào vòng lặp tuần hoàn số dư module , nên sẽ có vô số cặp cũng thỏa mãn . Điều đó cho thấy không nhất thiết cặp số cần chọn phải là cặp số đầu tiên của vòng lặp. Chúng ta sẽ xây dựng một chiến thuật mới nhằm giảm đi số lần tính ước chung lớn nhất. Xét vòng lặp module đầu tiên , chúng ta tìm kiếm một chỉ số thỏa mãn là bội của . Có thể khẳng định chỉ số này luôn tồn tại, thật vậy, đặt , luôn có thể tìm thấy thỏa mãn:
Từ tính chất * suy ra với $\alpha ,\beta $ bất kỳ. Chọn , ta có:
Tức cặp số thỏa mãn . Chúng ta chỉ mất nhiều nhất lần là có thể tìm được thỏa mãn - số lần tính GCD đã được giảm đi đáng kể.
Vẫn từ ví dụ trên, , , chọn , lần lượt tính toán , , , ... cuối cùng thu được là một ước nguyên tố của .
Thuật toán Pollard có thể cài đặt dễ dàng bằng ngôn ngữ Python như sau:
n = 7171
def gcd(a, b):
while b:
a, b = b, a % b
return a
# f(x) = x*x + 1
def f(i, n):
if i == 1:
return 1
return (f(i - 1, n) * f(i - 1, n) + 1) % n
def Pollard_p(n):
i = 1
p = 1
while p == 1:
x = f(i, n)
x_ = f(2 * i, n)
p = gcd(x - x_, n)
i += 1
return p
p = Pollard_p(n)
if p == n:
print("please choose another f(x)")
else:
print("p =", p)
Kết quả:
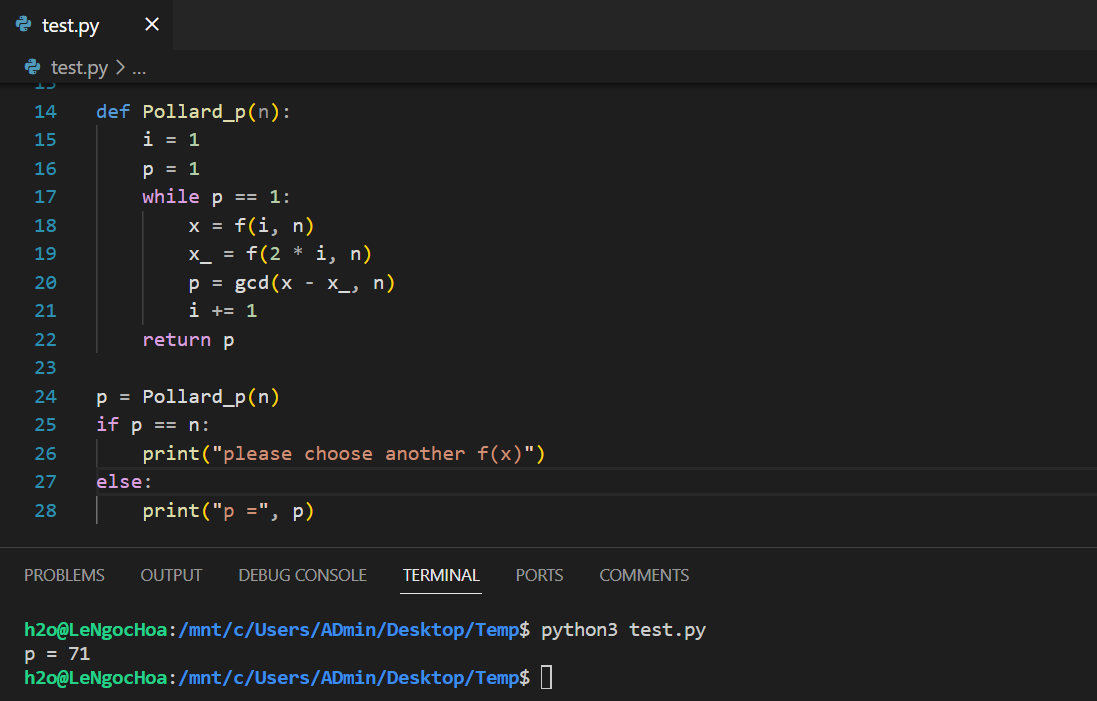
Tùy vào mỗi trường hợp, chúng ta có thể cài đặt thuật toán với các chiến thuật tìm kiếm cặp phù hợp.
2.2. Hàm và dãy số ngẫu nhiên
Sau khi hiểu về thuật toán Pollard , bạn đọc sẽ không khó để phát hiện thuật toán dựa vào "xác suất" để tìm ra ước nguyên tố của , trong đó việc chọn ra dãy ngẫu nhiên đóng vai trò quan trọng. Vậy thì, cần xác định hàm như thế nào để dãy thu được sẽ "sớm" đi vào một vòng lặp ?
Một cách chọn phổ biến nhất là . Với , quan sát giá trị đầu tiên của dãy ngẫu nhiên:
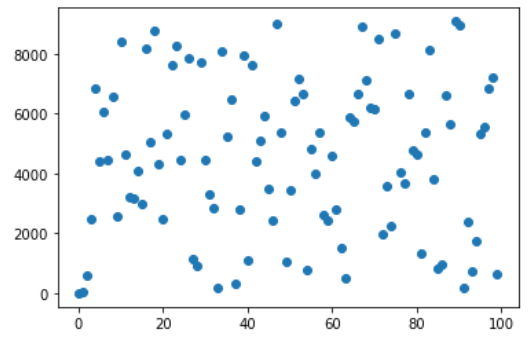
Các giá trị khá ngẫu nhiên và chưa thấy rõ quy luật, tuy nhiên, nếu đổi thành :
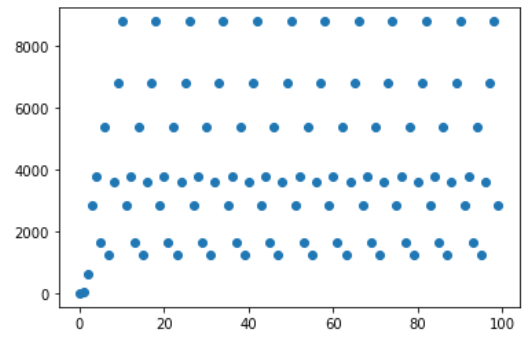
Bảng giá trị bắt đầu trở nên có quy luật! Bởi mỗi số đều được sinh ra dựa vào số ngay trước nó qua hàm , cũng bởi tính module, nên số lượng số sinh ra là có hạn, do đó sớm hay muộn cũng sẽ đi vào một vòng lặp . Chúng ta cần có "niềm tin" này khi thực hiện chọn hàm phù hợp với từng trường hợp của .
Chúng ta cùng xem xét challenge CTF về mật mã RSA, mã nguồn cung cấp được viết bằng Python như sau:
from Crypto.Util.number import getPrime, isPrime, bytes_to_long
flag = 'Viblo{****************************}'
nbits = 2048
gbits = 1000
g = getPrime(int(gbits))
while True:
a = getPrime(int(nbits * 0.5) - gbits)
p = 2 * g * a + 1
if isPrime(p):
break
while True:
b = getPrime(int(nbits * 0.5) - gbits)
q = 2 * g * b + 1
if p != q and isPrime(q):
break
N = p * q
e = 65537
def str2int(s):
return bytes_to_long(flag.encode())
with open('pubkey.txt', 'w') as f:
f.write(str(e) + '\n')
f.write(str(N) + '\n')
plain = str2int(flag)
c = pow(plain, e, N)
with open('cipher.txt', 'w') as f:
f.write(hex(c))
Nội dung file cipher.txt:
0x5cf9b2a6a0f5723dcd90e4e7cd8c2f4a115aa8e2d123eb949d4d1e4641a276c445b5a0dc5f3e7ae77cfacec09debc5544a32247885e383a6b11c82eaa794d3f23f0a73aa5a3cc760c7f132f2b2a5b74d57b8fd789f125a130f3e3bfc2854b60f51bc9d976f3e58f8c694cf4b2aa93a952e69df3d80d346ec65387dc7096d17e0a301ff6b25e5fa120ec4dce1c1429443940e3c38713ff5a43ee2e7403bad33195c5c418dcdae4ec7e60c44470759bc2c4688667c5c6e9f0443cd39aad077a4cc6e4b6bc6fd2fe2867b5d16c355ec02c68b0c81123cffb94222637b80888222b66b4311234cc5695028610c93d582384ecc0ea9931e26b5b4e73a54cfebc0fb3b
Nội dung file pubkey.txt:
65537
20902790268633126850940679053298116769870106633933056047845154148737759906850349907720879485630593331090207332245583521473134664307263774133558697957031694642194157647671844964402839468299788129346761280107832521466479427160024734846709374068332170121459314888809358316863795032578177090450355693844943882436399605171289629939417439079078271299240693557149051279583801809487720045200649857180919839745011714126062683953532293990025086093547019729918799593133102015844167158296181560011275838819713053780666492185682095297862014018657264790208019989335446936012947041060652330757324747617960007836606179355980236498609
Nhìn vào số có thể thấy cơ chế RSA này đảm bảo an toàn do độ dài khóa công khai lên tới bit. Tuy nhiên, chúng ta chú ý tới cách sinh hai số nguyên tố lớn trong đề bài:
nbits = 2048
gbits = 1000
g = getPrime(int(gbits))
while True:
a = getPrime(int(nbits * 0.5) - gbits)
p = 2 * g * a + 1
if isPrime(p):
break
while True:
b = getPrime(int(nbits * 0.5) - gbits)
q = 2 * g * b + 1
if p != q and isPrime(q):
break
Ở đây, challenge sử dụng số nguyên tố có độ dài bit, sinh ra hai số nguyên tố lớn theo công thức:
Cách sinh số đặc biệt này cho biết và tồn tại một ước nguyên tố chung là ( bit). Đây chính là điểm mấu chốt để tìm ra hướng đi bài toán phân tích số dài bit ra thừa số nguyên tố trong trường hợp này. Thật vậy, khi đó ta có:
Sử dụng module ta có:
Tham khảo mục THE FIRST STAGE OF THE ATTACK tại FURTHER ATTACKS ON SERVER-AIDED RSA CRYPTOSYSTEMS chúng ta sẽ chọn hàm:
Cách chọn này sẽ giảm độ phức tính toán xuống . Mã nguồn lời giải gợi ý bạn đọc có thể tham khảo:
from Crypto.Util.number import getPrime, isPrime, bytes_to_long, long_to_bytes
def gcd(a, b):
while b:
a, b = b, a % b
return a
def mapx(x):
# sử dụng module pow(x, n - 1, n) nhằm giảm tính toán
x = (pow(x, n - 1, n) + 3) % n
return x
def pollard_rho(x1, x2):
while True:
x1 = mapx(x1)
x2 = mapx(mapx(x2))
p = gcd(x1 - x2, n)
if (p == n):
print("fail")
return
elif (p != 1):
print("p: ", p)
print("q: ", n // p)
break
def main():
pollard_rho(1, 1)
return
n = 44327510143608652757309189121332002880736698826750814657928212799250989192533667090201158810441527941988339241953786693677345673674361495114190715248262185309157465424294779216031542945593633753442877226657245200617765607501935803024360190835150880116213395142289073140262609992858604295835861176915393471286050495813474776327352620577951619237771437380151233189336755447495103212957954178961674076787878537486516933808009793508283662417305262989135712933581661719965234419967031722873415515599146228798914453074940076094660682125563394179615976699753629942908617177026410858707681194686016943415767375769391168384273
main()
Kết quả thu được hai số nguyên tố và :
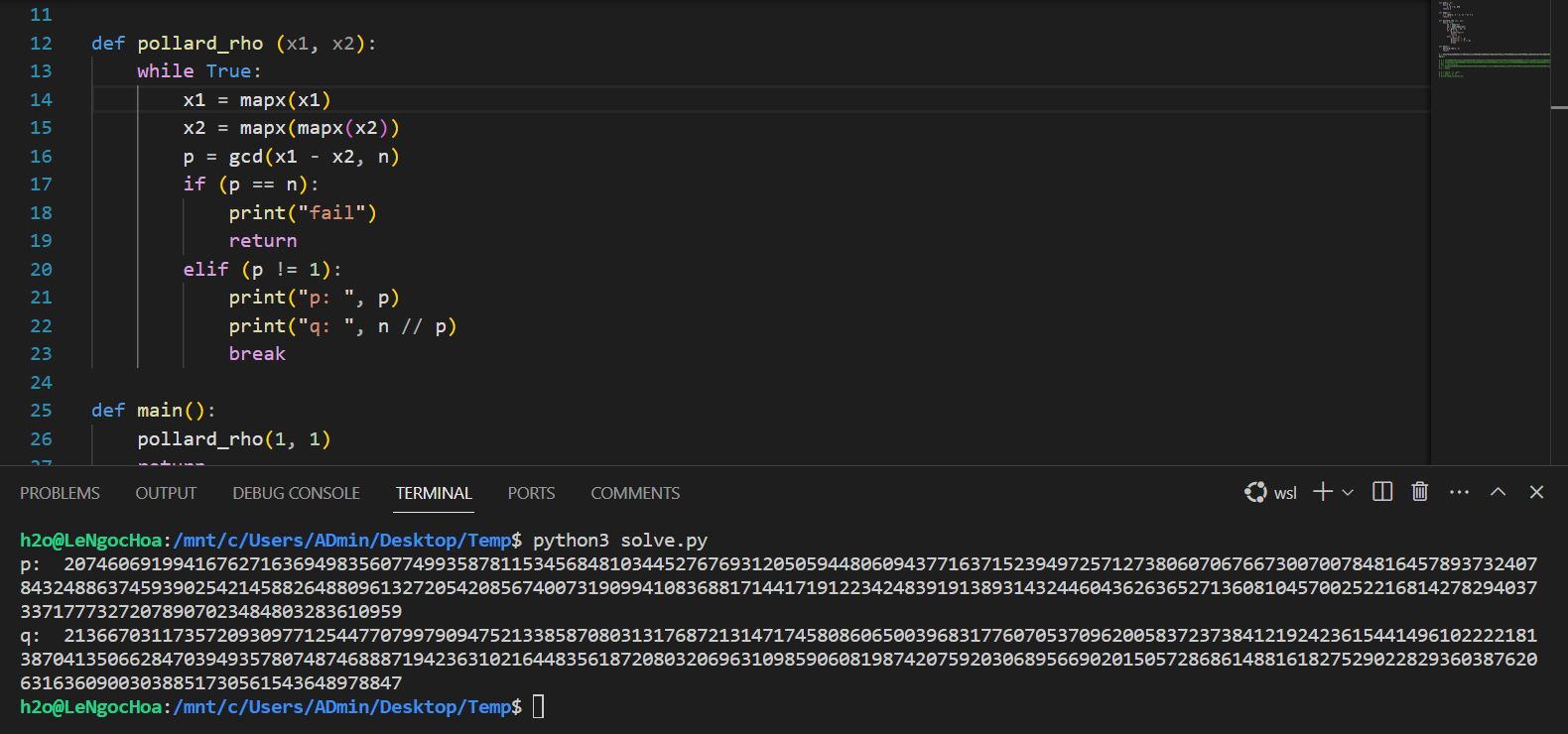
Tài liệu tham khảo
- https://en.wikipedia.org/wiki/RSA_(cryptosystem)
- https://www.amsi.org.au/teacher_modules/pdfs/Maths_delivers/Encryption5.pdf
- https://sites.math.washington.edu/~morrow/336_09/papers/Yevgeny.pdf
- https://en.wikipedia.org/wiki/Pollard's_p_−_1_algorithm
- https://www.geeksforgeeks.org/pollards-rho-algorithm-prime-factorization/
- https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.33.1333&rep=rep1&type=pdf
All rights reserved