2.9K 222 104

Đã đăng vào thg 9 27, 9:00 SA 6 phút đọc

194

Mật mã RSA - phần 2

III. Mật mã RSA - thực hiện

1. Kiến thức chuẩn bị

1.1. Số nguyên tố

Số nguyên tố là một khái niệm toán học quen thuộc chúng ta đã được tiếp xúc ở thời THCS. Một số tự nhiên lớn hơn $1$ được gọi là số nguyên tố nếu nó chỉ có hai ước dương duy nhất là $1$ và chính nó. Chẳng hạn, số $2$ chỉ có hai ước dương là $1$ và $2$ nên là số nguyên tố, số $5$ chỉ có hai ước dương là $1$ và $5$ nên là số nguyên tố, số $9$ là hợp số (không phải số nguyên tố) vì nó có nhiều hơn $2$ ước dương là $1$ , $3$ , $9$ .

Định lý vô hạn số nguyên tố: Từ thế kỷ III trước Công nguyên, nhà toán học Hy Lạp Ơ-Clit (Euclide) đã chỉ ra và chứng minh rằng tập hợp các số nguyên tố là vô hạn. Cách chứng minh rất đơn giản bằng cách sử dụng phương pháp phản chứng:

Giả sử có hữu hạn số nguyên tố lần lượt với giá trị tăng dần $p_1 < p_2 < ... < p_n$ . Xét số $A = p_1\times p_2\times ... \times p_n + 1$ là một hợp số (do $A > p_n$ ), do đó $A$ phải có một ước nguyên tố $p_i$ nào đó. Mặt khác $A = p_1\times p_2\times ... \times p_i \times p_{i+1} \times ... \times p_n + 1$ nên $A$ chia cho $p_i$ có số dư là $1$ . Điều này dẫn đến $1$ chia hết cho $p_i$ (mâu thuẫn). Như vậy có vô hạn số nguyên tố!

1.2. Hai số nguyên tố cùng nhau

Hai số tự nhiên được gọi là nguyên tố cùng nhau nếu chúng chỉ có duy nhất một ước chung là $1$ . Ví dụ: $7$ và $9$ là hai số nguyên tố cùng nhau, $6$ và $8$ không phải là hai số nguyên tố cùng nhau vì chúng có ước chung là $2$ .

Từ khái niệm trên, chúng ta có một hệ quả: Hai số nguyên tố khác nhau bất kỳ sẽ là hai số nguyên tố cùng nhau.

1.3. Hàm số Ơ-le (Euler) $\phi()$

Leonhard Euler (15 tháng 4 năm 1707 – 18 tháng 9 năm 1783) là một nhà toán học, nhà vật lý học, nhà thiên văn học, nhà lý luận và kỹ sư người Thụy Sĩ.

Hàm số Euler của số nguyên dương $n$ được ký hiệu là $\phi(n)$ . Với định nghĩa là số các số nguyên dương thỏa mãn đồng thời hai điều kiện:

Nhỏ hơn hoặc bằng $n$ .
Nguyên tố cùng nhau với $n$ .

Chẳng hạn, $\phi(9) = 6$ vì có $6$ số từ $1$ đến $9$ nguyên tố cùng nhau với $9$ là: $1,2,4,5,7,8$ .

Công thức tính tổng quát hàm số Euler: Với $p_1, p_2, ..., p_k$ là tất cả ước nguyên tố của $n$ , ta có:

$\phi(n) = n(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_k}) = n\prod _{p|n}(1-\frac{1}{p})$

Ví dụ: $\phi(9)=\phi(3^2)=9(1-\frac{1}{3})=6$ , $\phi(36)=\phi(2^2.3^2)=9(1-\frac{1}{2})(1-\frac{1}{3})=12$ .

1.4. Đồng dư Modular

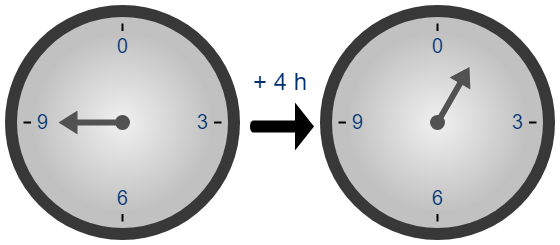
Hai số nguyên $a$ và $b$ được gọi là đồng dư với nhau theo module $n$ , nếu hiệu của chúng chia hết cho $n$ , hay nói cách khác, $a$ và $b$ có cùng số dư khi chia cho $n$ . Ký hiệu:

$a \equiv b \pmod n$

Ví dụ:

$3 \equiv 5 \pmod {2}\\ 9 \equiv 16 \pmod {7}\\ -13 \equiv 25 \pmod {19}$

1.5. Định lý Fermat nhỏ

Pierre de Fermat (17 tháng 8 năm 1607 tại Pháp – 12 tháng 1 năm 1665) là một học giả nghiệp dư vĩ đại, một nhà toán học nổi tiếng và cha đẻ của lý thuyết số hiện đại.

Định lý Fermat nhỏ phát biểu rằng: Nếu $p$ là một số nguyên tố, thì với số nguyên $a$ bất kỳ, $a^p - a$ sẽ chia hết cho $p$ . Ký hiệu bằng đồng dư thức, ta có:

$a^p \equiv a \pmod {p}$

Ví dụ, với $p=7$ , $a=4$ có $4^7 \equiv 4 \pmod {7}$ .

Hệ quả: Nếu $p$ là một số nguyên tố, thì với số nguyên $a$ bất kỳ và không chia hết cho $p$ ( $a$ và $p$ nguyên tố cùng nhau), thì:

$a^{p-1} \equiv 1 \pmod {p}$

Như ví dụ trên chúng ta còn có: $4^6 \equiv 1 \pmod {7}$ .

2. Sinh khóa

Trước khi có thể mã hóa và giải mã thuật toán RSA, chúng ta cần có bước tạo khóa, quá trình này đóng vai trò quan trọng vì ảnh hưởng trực tiếp tới tính an toàn trong toàn bộ giai đoạn truyền tin sau này. Yêu cầu cần tạo được cặp khóa public key và private key.

Bước $1$ : Chọn ra hai số nguyên tố $p$ , $q$ phân biệt và đủ lớn.
Bước $2$ : Tính $n=p.q$
Bước $3$ : Tính giá trị hàm Euler $\phi(n)=(p-1)(q-1)$
Bước $4$ : Chọn một số tự nhiên $e$ thỏa mãn $1<e<\phi(n)$ , đồng thời $e$ và $\phi(n)$ nguyên tố cùng nhau.
Bước $5$ : Tính $d$ thỏa mãn: $de\equiv 1 \pmod {\phi(n)}$

Sau khi hoàn thiện các bước trên, chúng ta thu được khóa công khai (public key) bao gồm số $n$ (số module) và $e$ (số mũ công khai, hay số mũ mã hóa), khóa bí mật (private key) bao gồm số $n$ (xuất hiện ở cả hai khóa), số $d$ (số mũ bí mật, hay số mũ giải mã).

3. Mã hóa

Thuật toán mã hóa RSA sẽ mã hóa thông điệp dưới dạng các phép tính toán học, tức thực hiện với các con số. Giả sử A cần truyền tải một thông điệp $P$ cho B, trước hết, A cần chuyển thông điệp dưới dạng một số nguyên $m$ , với điều kiện dạng mã hóa này có thể giải mã lại thành thông điệp ban đầu (A và B đã thảo luận trước sẽ sử dụng loại mã hóa này). Tiếp theo A sử dụng bộ puclic key $(n, e)$ thực hiện tính số $c$ :

$c = m^e\ \ \text{mod}\ \ {n}$

Số $c$ được tính bằng số dư của $m^e$ khi chia cho $n$ , cũng chính là thông điệp đã mã hóa cần truyền tải.

Khi B nhận được $c$ , B sử dụng bộ private key $(n, d)$ thực hiện tính lại số $m$ :

$m = c^d\ \ \text{mod}\ \ {n}$

Vì sao chúng ta có công thức tính lại số $m$ như trên? Bạn đọc theo dõi chứng minh như sau, ta có:

Từ công thức $c = m^e\ \ \text{mod}\ \ {n}$ có:

$c\equiv m^e \pmod{n}\\ \rightarrow c^d\equiv (m^e)^d \pmod{n}\\ \rightarrow c^d\equiv m^{de} \pmod{n}\ (*)$

Tiếp theo, chúng ta sẽ chứng minh: $m^{de}\equiv m \pmod{p}$ , hay $p|m^{de}-m$ ( $p$ là ước của $m^{de}-m$ ). Nếu $m$ là bội của $p$ thì điều này là rõ ràng. Ngược lại, nếu $m$ và $p$ nguyên tố cùng nhau, theo định lý Fermat nhỏ ta có:

$m^{p-1}\equiv 1 \pmod{p}$

Vì $de\equiv 1 \pmod {\phi(n)}$ nên $\phi(n)\ |\ de-1$ , hay $(p-1)(q-1)\ |\ de-1$ , suy ra $(p-1)\ |\ de-1$ . Đặt $de - 1 = t(p-1)$ thì:

$m^{de-1} = m^{t(p-1)} = (m^{p-1})^t\equiv (m^{p-1})^t\equiv 1^t\equiv 1 \pmod{p}\\ \rightarrow m^{de} \equiv m \pmod{p}\\$

Tương tự ta cũng có: $m^{de} \equiv m \pmod{q}$ . Do $p$ và $q$ là hai số nguyên tố cùng nhau nên $m^{de} \equiv m \pmod{pq}$ , hay $m^{de} \equiv m \pmod{n}$ . Từ đây kết hợp với $(*)$ ta có:

$m \equiv c^{d} \pmod{n}\\ \rightarrow m = c^{d}\ \ \text{mod}\ \ {n}$

Xem xét một ví dụ cụ thể: giả sử cặp số nguyên tố $(p, q)=(61, 53)$ , số $n=61\times 53=3233$ , $\phi(n)=\phi(3233)=(61-1)\times (53-1)=3120$ , chọn $e=17$ thỏa mãn $1<17<3120$ và $(e, \phi(n))$ là hai số nguyên tố cùng nhau, số $d=2753$ thỏa mãn $de\equiv 1 \pmod {\phi(n)}$ . Thông điệp cần mã hóa ở dạng chuỗi số nguyên m=1289. Tính thông điệp mã hóa c:

$c = 1289^{17}\ \ \text{mod}\ \ {3233} = 272$

Khi nhận được thông điệp mã hóa, người nhận có thể tính lại:

$m = 272^{2753}\ \ \text{mod}\ \ {3233} = 1289$

Bài tập dành cho bạn đọc:

Bài $1$ : Với khóa công khai $n=943$ và $e=7$ , thông điệp mã hóa $c=545$ , số mũ bí mật $d=503$ hãy tìm ra thông điệp gốc $m$ ?
Bài $2$ : Với khóa công khai $n=943$ và $e=7$ , thông điệp mã hóa $c=545$ , hãy tìm ra thông điệp gốc $m$ ?

Tài liệu tham khảo

Crypto RSA