I. Mở đầu

Mật mã học là lĩnh vực nghiên cứu các phương pháp để bảo vệ thông tin và dữ liệu khỏi bị truy cập trái phép. Trọng tâm của mật mã học chính là vấn đề an toàn và bảo mật dữ liệu.

Khi một thuật toán mã hóa được đưa ra, người ta thường đặt ra câu hỏi về mức độ an toàn của nó, rằng:

• Nó có khả năng bị "phá vỡ" hay không?
• Nếu có, thì phải mất bao nhiêu tài nguyên (thời gian, công sức, công nghệ) để làm điều đó?

Bởi vậy, các thuật toán mã hóa hiện đại thường được xây dựng dựa trên các vấn đề khó chứng minh trong toán học. Đưa việc "phá vỡ" một mật mã trở về việc chứng minh một vấn đề khó khăn trong toán học đã được biết và công nhận.

Một vấn đề khó khăn nổi tiếng trong toán học chính là việc phân tích một số nguyên lớn ra tích các thừa số nguyên tố. Khi số nguyên lớn được xây dựng sao cho chỉ có ước là số nguyên tố lớn, thì việc phân tích ngược lại trở nên vô cùng khó khăn. Vấn đề được thể hiện rõ trong thuật toán mã hóa RSA.

Tuy nhiên, theo thời gian, sự phát triển của công nghệ thông tin đã cải thiện đáng kể khả năng cũng như tốc độ tính toán của máy tính, dần đe dọa tới sự an toàn của bài toán này. Nhất là sự ra đời của máy tính lượng tử, đã thực sự khiến các nhà mật mã học trở nên lo ngại và mong muốn xây dựng một hệ mật mã dựa trên một vấn đề nan giải khác. Chính là một trong những nguyên nhân thúc đẩy sự ra đời của mật mã học trên lưới.

Tại sao lại là lưới? Lưới là một cấu trúc toán học được định nghĩa bởi một tập hợp các điểm trong không gian $n$-chiều, được sinh ra từ các tổ hợp tuyến tính nguyên của một tập hợp vector cơ sở. Các bài toán trên lưới thường liên quan đến việc tìm kiếm các điểm "ngắn nhất" hoặc "gần nhất" trong lưới, và chúng được chứng minh là rất khó giải quyết.

II. Một số khái niệm cơ bản và một số bài toán trên lưới

1. Vector và vector cơ sở

Chúng ta đã quen thuộc với các vector trong toán học từ cấp ba, thực ra chúng có tên đầy đủ hơn là các vector hai chiều, như $(1, 2)$, $(3, 7)$, ... Thực tế vector $u$ có thể tồn tại $n$ chiều và có dạng $u=(a_1, a_2, ..., a_n)$.

Vector cơ sở là một khái niệm quen thuộc trong Đại số tuyến tính. Có thể hiểu đơn giản các vector cơ sở là những thành phần nhỏ nhất tạo nên một không gian vector.

Một số tính chất quen thuộc nhắc lại:

$$u+v = (a, b) + (c, d) = (a+c, b+d)\\ u - v = (a, b) - (c, d) = (a-c, b-d)\\ k*u = k*(a, b) = (k*a, k*b)\\ u \cdot v = (a, b) \cdot (c, d) = a*c+b*d$$

Ví dụ, cho các vector $a=(1, 2, 3), b = (4, 7, 12), c = (2, 1, 9)$, có:

$\ \ \ \ 2*(3*a+2*b)\cdot 4*c$ $=2*(3*(1, 2, 3)+2*(4, 7, 12))\cdot 4*(2, 1, 9)$ $=2*((3, 6, 9)+(8, 14, 24))\cdot (8, 2, 18)$ $=2*(11, 20, 33)\cdot (8, 2, 18)$ $=(22, 40, 66)\cdot (8, 2, 18)$ $= 22*8+40*2+66*18$ $= 1444$

2. Kích thước của vector (size of vector)

Kích thước (hay độ lớn) của vector $u=(a_1, a_2, ..., a_n)$ được ký hiệu là $||u||$, được tính bằng:

$$||u||=\sqrt{a_1^2+a_2^2+...+a_n^2}$$

Ví dụ, với vector $u=(1,2,3,4)$ có kích thước là:

$$||u||=\sqrt{1^2+2^2+3^2+4^4}=\sqrt{30}$$

3. Lưới (lattice)

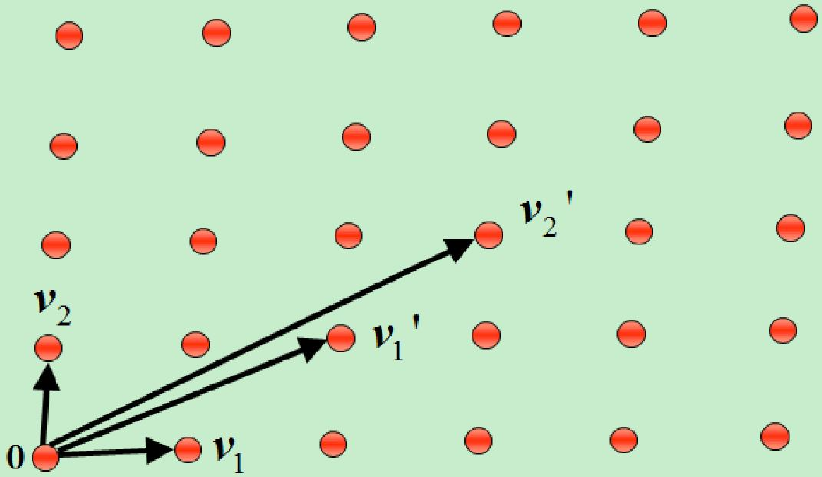
Dựa vào khái niệm không gian vector, chúng ta có thể tiếp cận định nghĩa về lưới như sau: Xét trong không gian tuyến tính $n$ chiều, có hệ $m$ vector cở sở độc lập tuyến tính là $v_1, v_2, ..., v_m\in R^n$ với $(m\leq n)$, chúng sinh thành một tập các vector với hệ số nguyên $a_1, a_2, ..., a_m$ tạo nên lưới là:

$$L=\{a_1v_1 + a_2v_2 + ... + a_mv_m: a_1, a_2, ..., a_m \in Z\}$$

Mỗi vector trong tập $L$ tương ứng với một điểm trên lưới. Có thể hiểu lưới cũng giống như một vector không gian với hệ số nguyên.

4. Cơ sở lưới (Lattice basis)

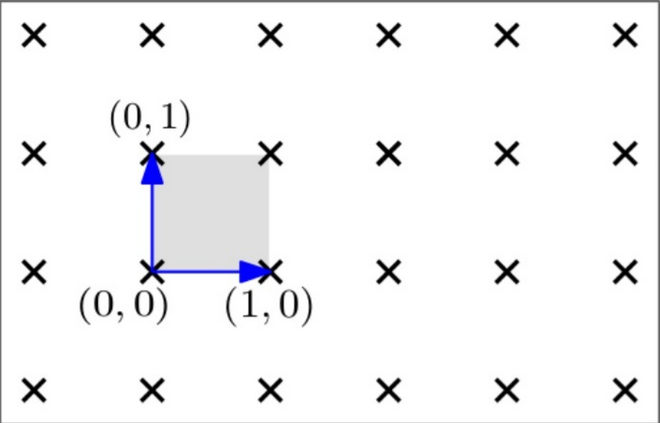
Cơ sở lưới chính là tập các vector cơ sở tạo nên lưới. Ví dụ xét một lưới hai chiều có cơ sở lưới là hai vector cơ sở $(0, 1)$ và $(1, 0)$. Với điểm bất kỳ $(a, b)$ trong lưới được tạo thành bởi hai vector cơ sở này:

$$(a, b) = a\times (1, 0) + b\times (0,1)$$

Lưu ý rằng một lưới có thể có nhiều cơ sở lưới khác nhau, và số lượng vector cơ sở trong các cơ sở lưới là như nhau.

Một số tính chất:

• Linear independence: Các vector cơ sở phải là độc lập tuyến tính, nghĩa là vector bất kỳ trong tập hợp này đều không thể biểu diễn được bằng tổ hợp tuyến tính của các vector khác.
• Spanning: Các vector cơ sở phải đủ để tạo thành điểm bất kỳ trong lưới.

5. The Shortest vector problem (SVP)

Đây là bài toán tìm Vector có độ dài nhỏ nhất trong $\mathcal{L}$.

Độ dài của Vector thường theo độ dài Euclid.

6. Trực giao Gram–Schmidt

Ta sẽ biến đổi hệ $(a_1,a_2,...a_n)$ thành hệ $(b_1,b_2,...b_n)$ với hệ $b_i$ là hệ trực giao.

Hệ số Gram-Schmit:

$$u_{i,j} = \frac{\langle a_i,b_j \rangle}{\langle b_j,b_j \rangle}$$

Trực giao Gram hệ $(a_1,a_2,...a_n)$ được thực hiện như sau:

1. $b_1=a_1$
2. $b_2 = a_2 - proj_{b_1}(a_2)$
3. $b_i = a_i - \sum_{i=1}^{j-1}u_{i,j} b_i$

7. LLL Basic Reduction

Cho hệ cơ sở $(b_1,b_2,...b_n)$ và hệ trực giao $(b_1^*,b_2^*,...b_n^*)$

Cở sở này được gọi là "LLL Reduced" khi thỏa mãn

1. $\forall 1\ \leq i \leq n, j<i$ thì $u_{i,j}<\frac{1}{2}$
2. $\forall 1\ \leq i \leq n$ thì

$$\delta|b_i^*|^2 \leq |u_{i+1,i}~b_i^*+{b_{i+1}^*}|^2=u_{i+1,i}^2~|b_i^*|^2+|{b_{i+1}^*}|^2$$

Lưu ý: $\delta$ thỏa mãn $\frac{1}{4}<\delta<1$ và thường có giá trị $=\frac{3}{4}$

Minh hoạ mã giả cho giải thuật trên:

def LLL(B, delta):
    Q = gram_schmidt(B)

    def mu(i, j):
        v = B[i]
        u = Q[j]
        return (v * u) / (u * u)

    n, k = B.nrows(), 1
    while k < n:
        # Length reduction step
        for j in reversed(range(k)):
            if abs(mu(k, j)) > 0.5:
                B[k] = B[k] - round(mu(k, j)) * B[j]
                Q = gram_schmidt(B)

        # Swap step
        if Q[k] * Q[k] >= (delta - mu(k, k - 1)**2) * (Q[k - 1] * Q[k - 1]):
            k = k + 1
        else:
            B[k], B[k - 1] = B[k - 1], B[k]
            Q = gram_schmidt(B)
            k = max(k - 1, 1)

    return B

Vậy thuật toán LLL sẽ làm gì, hiểu một cách đơn giản nhất là nó sẽ trả về một cơ sở chứa các Vector nhỏ nhất (Chính là LLL Reduced), khi đó các Vector trong cơ sở này sẽ là lời giải cho bài toán SVP mà đã minh hoạ trên.

Tài liệu tham khảo

• https://cryptohack.org/challenges/post-quantum/
• https://en.wikipedia.org/wiki/Lattice-based_cryptography